Overview

Regular expressions (regex) are a fun topic in computer science. I love revisiting the fundamentals every so often, so I read https://qntm.org/re_en recently. It is a great practical primer on regex. I’d recommend it to beginners and advanced engineers alike.

Backreferences

One of the most powerful regex techniques are backreferences. They allow you to match text that was previously matched by a capture group. You refer to previous groups using their index.

Example

Let’s assume you want to match the strings aa, bb or cc. A sufficient expression is ^(aa|bb|cc)$. The equivalent using a back expression is ^([a-c])\1$. The text from the group ([a-c]) is referenced by the 1th capture group using \1.

The zeroth capture group is the entire string, which is why the 1th is used. You can use backreferences to different capture groups in the same regex (\1, \2, etc).

Directed Acylic Graph

A directed acylic graph (DAG) has the following properties:

• all edges are directed
• no cycles are present in the graph (you cannot start at a node n and find a path back to n)

When you have a DAG, you can define a topological ordering of its vertices. It is a list of vertices such that for every edge in the graph a -> b, the node a comes before node b in the graph.

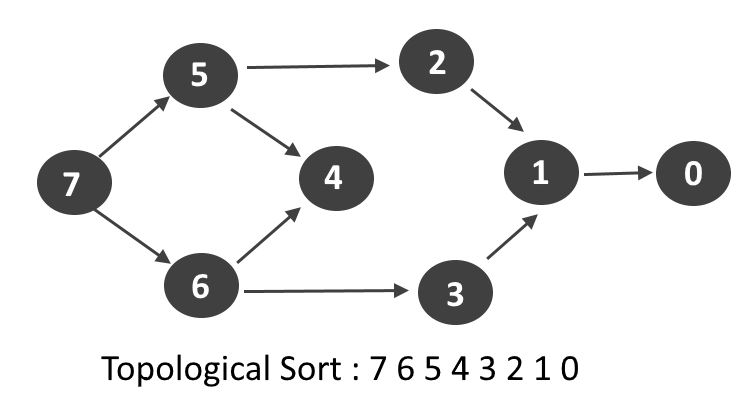
A classic graph theory problem is finding a path between two nodes. Using what we know about backreferences and DAGs, we can try and solve this using regular expressions.

Problem

Given a DAG, find a path between two nodes using a regular expression(s).

Encoding

Graphs are typically represented using a 2D matrix or adjacency lists. Regular expressions operate on strings. To encode a graph to a string, first get a topological ordering of the vertices in the graph. For the graph above, one such ordering is is a b c f j x y z.

Next, join each vertex with a string containing each vertex it has an edge to. For our graph, this is abcf bh cj fj jxy x yz z.

Now that we encoded the graph into a string, we can use regular expressions to try and extract a path from it.

Using Regex to extract a path

To find a path from a to j, one of a’s edges must be used (bcf). Then, for the first edge chosen, that must also have an edge leading to another vertext which leads to z. We can represent this idea in regex. Assuming the length of the path is 2, we can use a\w*(\w).*\s\1\w*j$.

Let’s digest this:

• a : We start with our first vertex
• \w*(\w) : We match a single vertex that a has an edge to.
• .*\s\1 : We scan the rest of the string until we find whitespace followed by the previous vertex (\1).
• \w*j : Ensure that the vertex has j has a neighbour.

The encoding of the string is important. If the vertices were not topolgically sorted, we may not have found a path. The regex looks forward for the next vertex to continue the path. If that it wasn’t forward but behind, this would not work. The encoding cj fj abcf bh jxy x yz z would not let us find a path from a -> j because cj and fj are behind it.

To extend, for paths of our lengths, we continually add sections of \w*(\w).*\s\1 where \1 changes to represent whatever the previous matching group index is.

The exact length of a matching path may not be known. My current solution generates regular expressions of lengths [1, # of verticies] and tries to find a match in any. However, I am sure you could generate one monster expression instead.

My current solution to the problem can be seen at https://gist.github.com/dang3r/f2434de0a167ecfb0b90f48be7d6df67

Why?

I would never suggest using this in any production setitng. However, it was a fun problem and helped me dive deeper into regex and a bit of graph theory. Learning through problem solving is my most effective way to learn.